A Reaction Drive

Sep 5, 2019

A Reaction Drive

A Reaction Drive

Powered by External Dynamic Pressure

This article originally appeared in the Journal of the British Interplanetary Society (JBIS).

JBIS Vol 72 No.5 May 2019 p. 146 – 152

Click here to download a PDF version

JEFFREY K. GREASON, Electric Sky, Inc., 602 North Baird St., Suite 200, Midland, TX, 79701, USA

email jeff.greason@el-sky.com

A new class of reaction drive is discussed, in which reaction mass is expelled from a vehicle using power extracted from the relative motion of the vehicle and the surrounding medium, such as the solar wind. The physics of this type of drive   are reviewed and shown to permit high velocity changes with modest mass ratio while conserving energy and momentum according to well-established physical principles. A comparison to past propulsion methods and propulsion classification studies suggests new mission possibilities for this type of drive. An example of how this principle might be embodied in hardware suggests accelerations sufficient for outer solar system missions, with shorter trip times and lower mass ratios than chemical rockets.

 

Keywords: Propulsion, Reaction drive, Solar wind, External power, Dynamic pressure

1     INTRODUCTION

In the sixty years since the first interplanetary spacecraft (Luna 1), scientific probes have been flown to all the large bodies in the solar system, and, after decades of flight time, the twin Voyager 1 and 2 spacecraft are entering the boundary between the solar system and interstellar space. However, missions to the outer solar system are still very difficult, with long trip times, even with use of gravity assist maneuvers.

Substantial reductions in trip times to the outer solar system or for interstellar precursor missions are difficult for fundamental physical reasons. Fast trips imply high velocities: a constant speed of 100 km/s is only ~20 AU/year, beyond any demonstrated capability (though achievable with a close-solar flyby Oberth maneuver). Fast trips also imply that acceleration cannot be too small: a 29 AU trip (Neptune from Earth) of 100km/s peak velocity requires a constant acceleration of at least 0.005 m/s2 to achieve a two-year flight time (ignoring Solar gravity), otherwise too much time is spent in acceleration and braking to take advantage of high speed.

With rocket propulsion, high velocity implies either high mass ratio (expense) or high exhaust velocity (high specific energy of the propellant). High acceleration implies high specific power, which is why electric rockets have not been able to overcome these limitations. Nuclear propulsion systems offer high specific energy, but whether they can combine high specific energy with high specific power remains to be demonstrated.

These well-known challenges have led to exploration of various types of ‘sail’ which use either the photons or the solar wind particles as an external source of momentum to harvest [1,2]. Most of these approaches offer low accelerations because of the large collection areas required, but at least one, the “plas- ma magnet” [3], offers useful accelerations by using large-scale magnetic fields from small generators.

This work was motivated by the realization that while such sails offer near-term prospects for acceleration to high heliocentric velocities away from the sun (hundreds of km/s), that there is no current propulsion system which permits braking from those velocities or sunward acceleration.

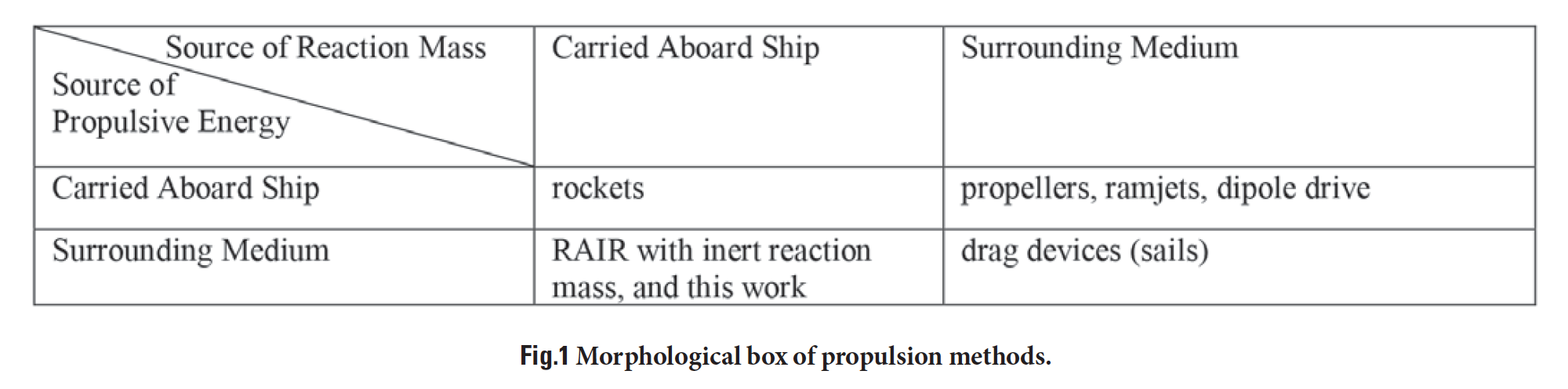
The widely known methods of accelerating and decelerating in a surrounding medium, including propellers, ramjets, turbojets, rockets, parachutes, and sails, form distinct classes of propulsion. Energy can be provided by the vehicle or by the surrounding medium, while reaction mass can be carried aboard or harvested from the surrounding medium. By classifying propulsion systems in this way (a “morphological analysis”, following the methods of Zwicky [4]), a promising form of propulsion is identified, in which the reaction mass is carried aboard the vehicle, but the energy to expel that reaction mass is provided by the passage of the vehicle through the medium. This was anticipated by Alan Bond [5] in the limit of high-speed operation of ram-augmented interstellar rockets in which inert, rather than energetic, reaction mass could be used. The principle however is useful in contexts beyond the original application. We review the physics of the classical systems, and then explore the physics of this alternative form of propulsion. Finally, some examples of how this might be realized in an implementable device for fast transportation in the interplanetary medium are given.

2  REVIEW OF CLASSICAL APPROACHES AND THEIR PHYSICS

 A review of the fundamental physics of existing propulsion is needed to understand how this method differs. The methods are grouped depending on whether propulsive energy is internally carried or externally harvested, and whether reaction mass is internally carried or externally harvested. Beginning with the equations of those well-known systems also provides the basis for deriving the physics of the new approach.

2.1  Propeller Systems (internal energy, external reaction mass)

 

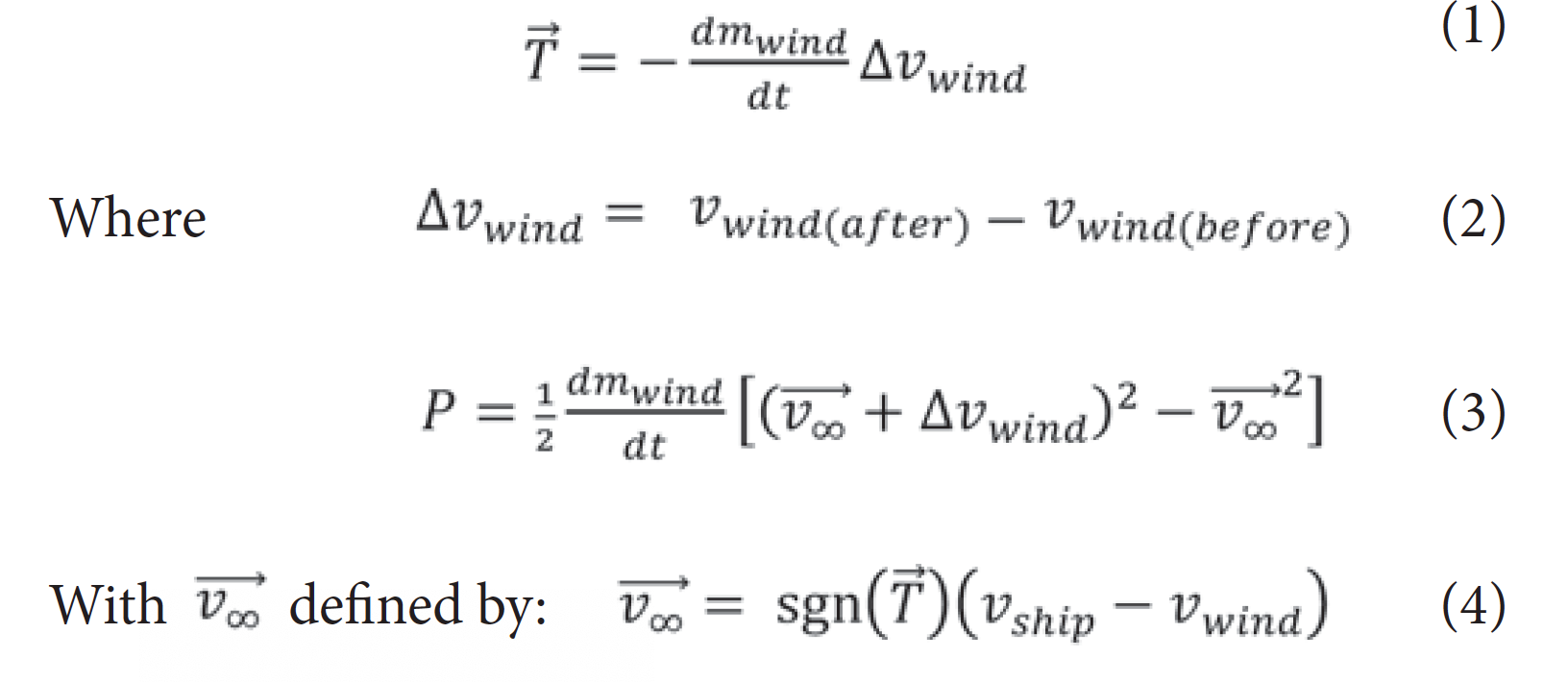
This simplified form illustrates that the higher the freestream velocity, the more power is required for a given thrust, which is why rockets tend to dominate at higher speeds even when used within the atmosphere [8]. Recently, systems extending the propeller principle to the interplanetary plasma as a medium have been suggested, with the same general physical principles [9,10].

2.2  Rockets (internal energy, internal reaction mass)

As the limitations of propeller systems in reaching high velocities became apparent, the application of the rocket principle became attractive. All rocket-type systems, regardless of power source, have broadly similar behavior. They are governed by the rocket equations [11].

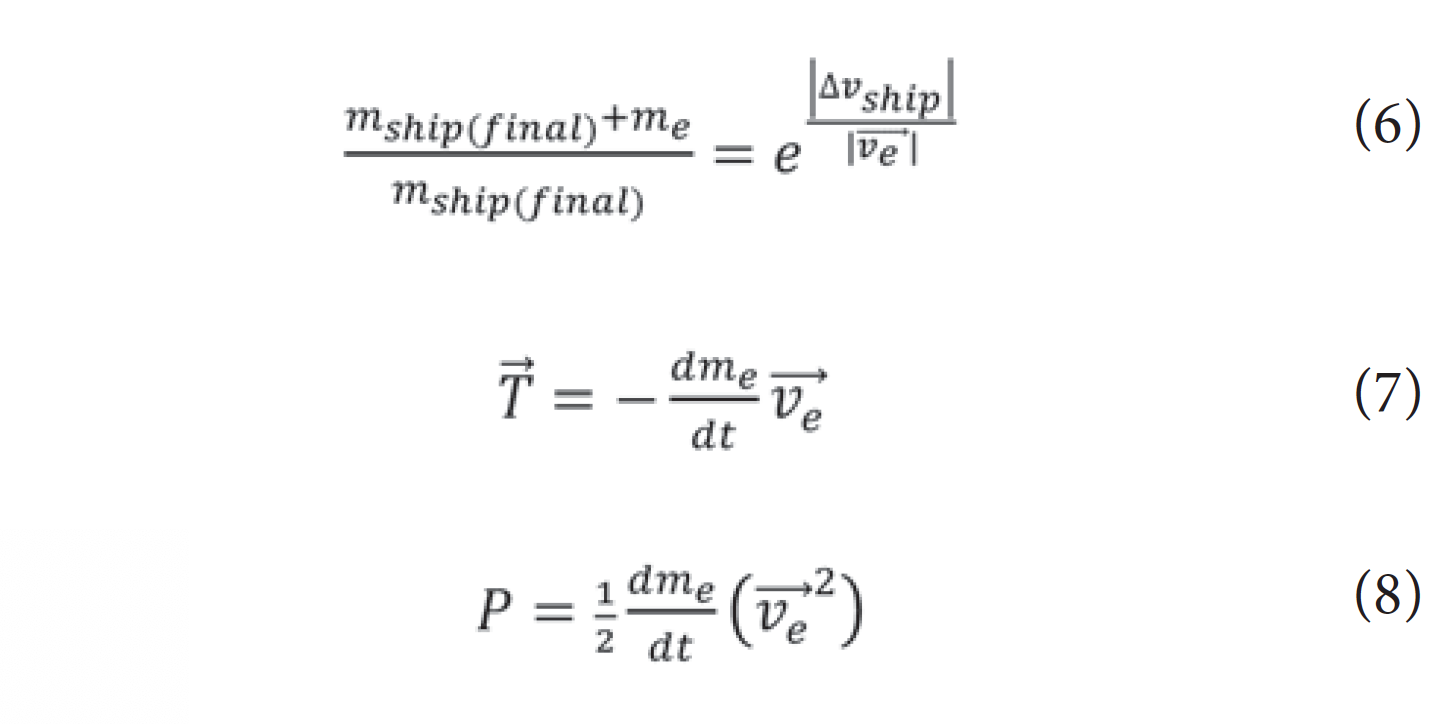
Where the surrounding medium is moving relative to the ship, the application of drag can be useful, either to accelerate downwind (simple sails) or to brake a preexisting velocity (parachutes and aerobrakes). In these cases, any energy required is provided by (or carried away by) the surrounding medium, and the reaction mass is also formed by the surrounding medium. Drag devices are usually considered a distinct class of device from propellers and rockets.

One motivation for the current work is the recent proliferation of proposals for using the interplanetary or interstellar plasma as a medium for drag devices, which show that in spite of the low density (~10-20 kg/m3 for the interplanetary medium at 1 AU, as low as ~10-22 kg/m3 in hot plasma interstellar regions), useful accelerations can be achieved through electromagnetic interactions. This was first conceived as a magnetic sail or magsail [1], and more recently as an electric sail [2]. A particularly high drag to mass configuration is the “plasma magnet” magnetic sail, which offers a streamtube capture area far larger than the physical dimension of the coils involved in the device [3]. Fundamentally these are all drag devices, although the capture area, and hence the value of

involved at a given phase of flight, differ significantly. As drag devices, they provide thrust as in Equation 1 above, although the power, as shown in Equation 5, is then delivered to the ship rather than being provided by the ship. Power can be large in cases where

is large.

These drag devices have great promise for certain missions including outer solar system flybys or missions to the heliosphere boundary, and for braking systems for interstellar missions. By harvesting thrust power from outside sources, they can operate at levels of thrust power well beyond our current ability to provide propulsive energy storage aboard a spacecraft. Unfortunately, by the nature of a drag device, they can only accelerate “downwind”, and so can only partially reduce propulsion requirements in cases such as outer solar system orbiters. Many desirable missions require thrust both for acceleration and for deceleration (stopping and starting a fast transit).

It is worth noting that the ideal Bussard Ramjet [12] while not a ‘drag’ device, would also fall into this category of both the energy and the reaction mass being provided externally. The many practical difficulties in the implementation of such a device have been discussed in the literature beginning with [13].

2  THE REMAINING OPTION

A morphological analysis (Zwicky box [4]) of the suite of propulsion devices shows that there is a remaining class of reaction devices: one in which the reaction mass is carried aboard the ship and is expelled using the power extracted from the flow of the surrounding medium. This approach does not appear in the common surveys of the propulsion art [4,11,14], and the first mention of it appears to be in Bond’s discussion of the Ram-Augmented Interstellar Rocket [5], in which he points out that in the limit of high-speed operation, the energy contribution of the rocket propellant becomes nearly negligible and that indeed the RAIR could then function with inert reaction mass. However, there is no reason to limit the application of this principle to that particular implementation – indeed, as noted in [5], the process of ram-compression of the interstellar medium to densities where RAIR operation is plausible introduces inefficiencies (parasitic drag) which make that particular implementation difficult (Fig.1).

The key element of the type of drive contemplated here is that if the interplanetary or interstellar medium is dense enough to provide meaningful drag using plasma techniques, then it can be a source of power as well as drag. The medium can do mechanical work on a system, thus extracting power from the ‘wind’: analogous to a ram air turbine in atmospheric flight. Since in doing so the vehicle experiences drag, the fundamental equations of this class of propulsion system must be examined to determine its performance and behavior. There is no need in general to compress the interstellar or interplanetary medium to operate a drive on these principles; one need only extract energy from it to expel onboard inert reaction mass.

2.1  Nomenclature of This Type of Drive 

The nomenclature for such a device is not obvious. While it might be classified under the broad heading of ‘jet propulsion’ since it expels reaction mass, that classification also includes propellers, which are broadly recognized as different from rockets. As will be seen, the governing equations are also different from rockets (the rocket equation does not apply), so calling them some form of ‘rocket’ seems misleading. And since they produce thrust and consume propellant mass, ‘sail’ hardly seems appropriate. Following Zwicky, one might think of them as a ‘dynamic-pressure-powered mass driver’, but that is rather clumsy. Bond [5] suggests this as the high-speed, inert reaction mass limit of a ram-augmented interstellar rocket, but since in the general implementation, there is neither ram-pressure recovery, nor a rocket, nor augmentation, nor interstellar flight, that nomenclature seems ill-suited to the general case. This propulsive principle might be called a “wind drive”, or, “ram drive”, but using the common abbreviation q for dynamic pressure [15] suggests the name q-drive – which is the name used in the balance of this text.

2.2  Momentum and Energy Conservation

 Fundamentally, as a propeller takes advantage of the fact that at low speed, it takes little energy to make thrust, the q-drive principle takes advantage of the fact that at high speed, a small drag device can extract a great deal of power. The power from a wind-harvesting device follows Equation 5, while the power required to expel stored reaction mass follows Equation 8. In the ideal case of no losses and no parasitic drag, this leads to the following fundamental equations (derived in the Appendix) for minimum use of reaction mass:

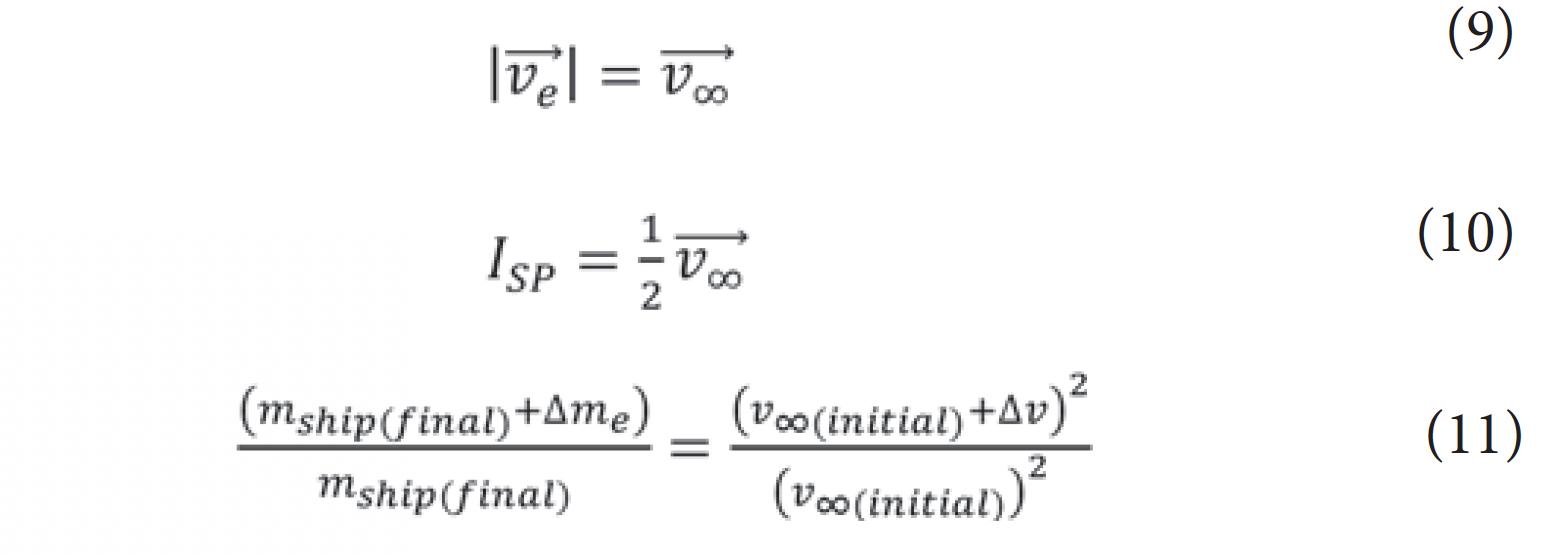
At first glance, the q-drive principle appears to offer “something for nothing”. Propellant is expended but where does the energy come from? The answer is that the energy comes from the loss of velocity of the reaction mass to the surrounding medium. One may think of it as an inelastic collision between the expended reaction mass and the surrounding medium, where the resulting change in energy is carried away by the ship. In this sense, it is very reminiscent of the Oberth effect [16], in which there are also three masses involved: the ship, the exhaust mass, and a planet. The q-drive principle is much more flexible, however, since it uses the surrounding medium as the third mass, and so the q-drive is not restricted to operation near a gravitating body.

Finally, while the analogy is imperfect, this has some similarity to the method by which sailing vessels on Earth can sail upwind. In that case, the energy is derived from the motion of the surrounding air, and the “reaction mass” is provided by the action of the keel on the water. In space, we can achieve comparable results by expelling reaction mass from the vehicle.

4  EXAMPLE IMPLEMENTATIONS

The propulsive principle outlined in this paper could apply to high-speed atmospheric flight or to travel in the interplanetary or interstellar medium. However, to determine whether the q-drive principle has real engineering utility, some concept of how this principle can be embodied in hardware is helpful.

Furthermore, the question of whether the acceleration achieved is useful for fast transits can only be assessed in the light of a hardware implementation. Realize that these examples are just that: guideposts for two ways to apply the q-drive principle to real hardware. The first example is presented only because it is physically very simple, and so enhances understanding of the physical principles. The second example may be a practical implementation, with acceleration > 0.02 m/s2.

4.1  Continuous Mode, Electric Field Power Extraction

4.2   Pulsed Mode, Magnetic Field Power Extraction

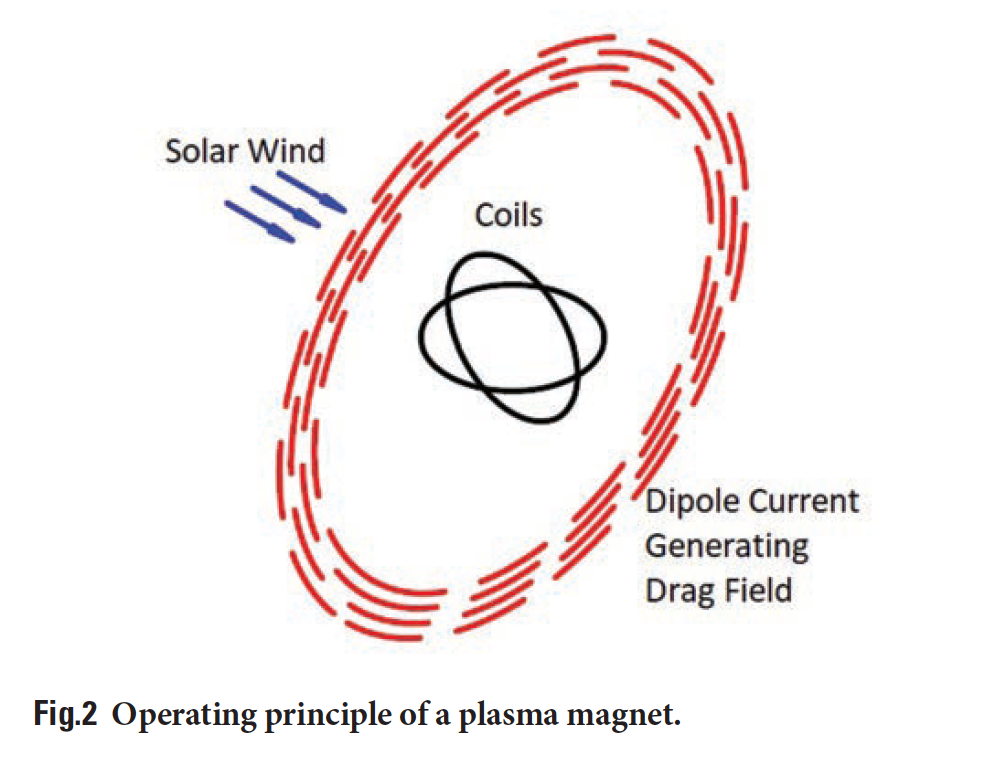
For accelerations that enable fast transits, a method of extracting power from the solar wind is needed that provides a high drag-to-mass ratio, and it seems likely that a low parasitic drag is also important. In atmospheric applications, rotating devices (windmills, anemometers) are used to draw power from the wind, and magnetic field analogies of both are possible, but the relatively low lift-to-drag ratio of magnetic fields in plasma suggests these approaches may have high parasitic drag. A useful approach may lie in a linear, reciprocating motion of a magnetic field, where essentially all the drag goes into pushing on a moving field. High drag-to-mass is achievable using the plasma magnet approach [3].

The basic principle of the plasma magnet, illustrated in Fig. 2 overleaf, is that a rotating magnetic field, driven by alternating current in a crossed pair of coils, creates a circulating current in the plasma, and that current then expands in radius until it creates a dipolar magnetic field much larger than the physical coils.

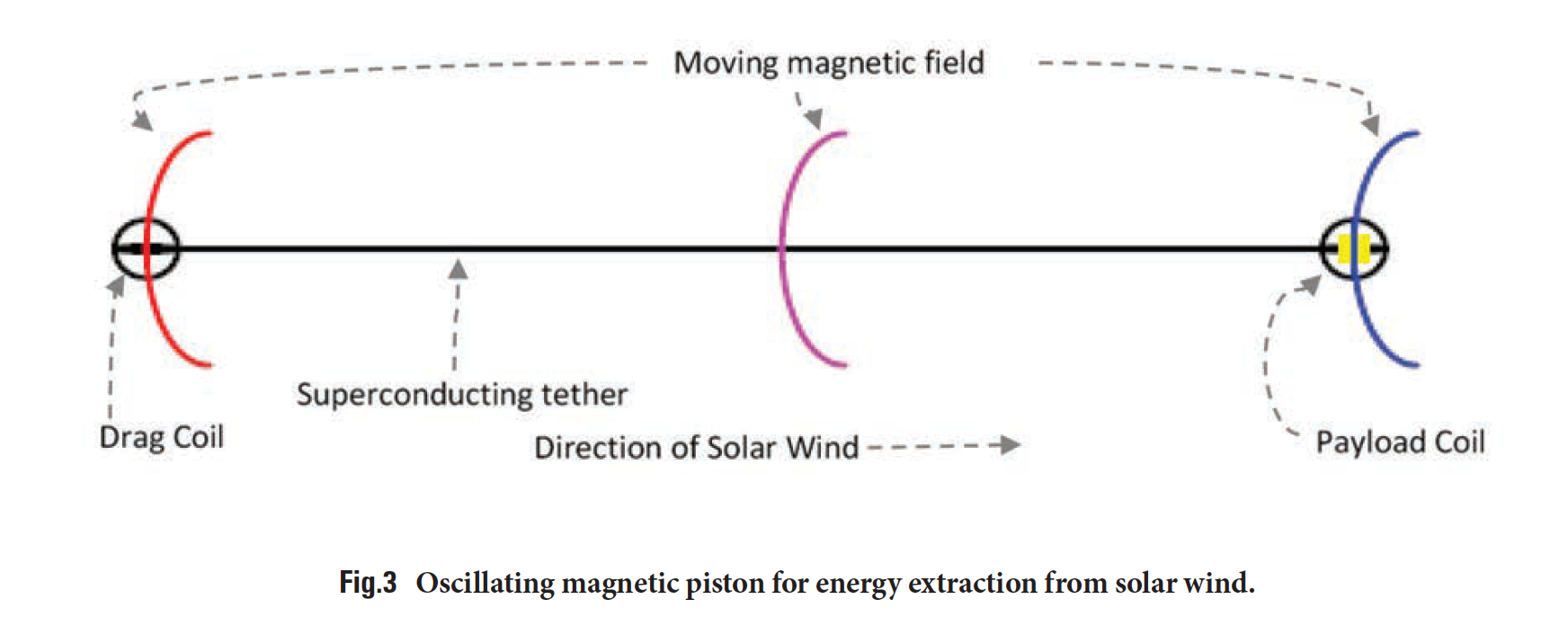
If such a field is turned on and the generating coils are attached to a tether, the tether will be pulled by the solar wind, which could rotate the shaft of a conventional generator. Then, the field could be turned off, the tether reeled back in, and the cycle repeated. In principle this approach of mechanically moving the field coils in a reciprocating manner would extract power, and it illustrates the principle involved, but the mechanical motions would be too slow to provide adequate power-to-mass ratio. We need a more rapid motion of the field, which can be achieved by replacing the reciprocating motion of the coils carrying the magnetic field with the reciprocating motion of the magnetic field itself.

In the approach illustrated in Fig.3, a pair of plasma magnet generating coil sets are used, separated by a tether with wires to transfer power from one set of coils to the other. Initially, the windward coil set is energized and the solar wind pushes on it, transferring the energy in the dipole field to the leeward coils. During the power stroke, energy is extracted from the wind, which can be used to power an electric thruster to expel reaction mass. A third coil set, omitted from the illustration for clarity but located at the windward end with a closed (toroidal) configuration that does not generate a magnetic field outside the coils, receives the energy on the return stroke, so that drag is only pushing on the field during the power stroke. Then, the energy is again transferred to the windward coil, and the cycle repeats.

A detailed design would be required to estimate mass but a sizing study, based on peak currents in superconducting MgB2

tapes at 20K [20-22] of 2.5 x108 A/m2, suggests that accelerations in the 0.025-0.05 m/s2 range may be feasible using this approach. The long tether, carrying oscillating currents in the 1 kHz range from end to end, modulated by a reciprocating frequency in the 20 Hz range, is admirably suited to form a Wideröe style [23] ion accelerator, thus providing an integrated method for converting the resulting electric power to thrust.

2  CONCLUSION

 A new class of reaction drives appears capable of generating vehicle velocities greater than those practical for propeller or rocket devices. The basic principles of this drive are those employed in the “inert reaction mass, high-velocity limit” of the Ram-Augmented Interstellar Rocket, but they do not require that particular implementation, nor do they require fusion technology, and by exploiting the solar wind, they are particularly useful for interplanetary flight.

 

A conceptual design suggests that, by using plasma magnet techniques, such a drive could offer accelerations and mass ratios sufficient for rapid transits to the outer solar system.

To explore further, the analysis of the physics involved needs to be extended in two ways. First, the analysis needs to include the effects of efficiencies in power conversion and parasitic drag, to assess whether the approach is practical. Second, to extend the application of this technique for inner solar system missions, the theory needs to be extended to include thrusts that are not parallel to the drag vector, which would enable a wider range of maneuvers.

This paper begins to examine routes for embodying this type of reaction drive in hardware. To assess the achievable accelerations, designs will need to be carried to a level of detail at which masses can be estimated credibly.

 

Acknowledgments

While this work was developed without sponsorship  from any organization, the author thanks the Tau Zero Foundation and the many researchers who have participated in the NASA Institute for Advanced Concepts for their work in advanced propulsion, elements of which inspired the investigation leading to this work. Thanks also to the reviewers at JBIS who suggested important prior art to include.

Appendix A

References

  1. R. Zubrin and D. Andrews, “Magnetic Sails and Interplanetary Travel,” 25th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, AIAA 89- 2441, AIAA, Washington, DC, 1989.
  2. P. Janhunen, “Electric Sail for Spacecraft Propulsion,” AIAA Journal of Propulsion and Power, 20(4), 2004, pp 763-764.
  3. J. Slough and L. Giersch, “The Plasma Magnet”, 41st AIAA/ASME/ SAE/ASEE Joint Propulsion Conference, AIAA 2005-4461, AIAA, Washington, DC 2005.
  4. F. Zwicky, “Fundamentals of Propulsive Power,” International Conference for Applied Mechanics, Paris, September 1946. Collected in Morphology of Propulsive Power, Society for Morphological Research, Pasadena, 1962, p. 37-47.
  5. A. Bond, “An Analysis of the Potential Performance of the Ram Augmented Interstellar Rocket”, JBIS, 27, 1974, pp. 674-685.
  6. W. J. M. Rankine, “On the Mechanical Principles of the Action of Propellers,” Transactions of the Institution of Naval Architects, 6, 1865, pp. 13-39.
  7. W. E. Froude, “On the Part Played in Propulsion by Differences of Fluid Pressure,” Transactions of the Institution of Naval Architects, 30, 1889, pp. 390-405.
  8. E. Sänger, Raketenflugtechnik, R. Oldenbourg Verlag, Muich-Berlin, 1933, in translation as “Rocket Flight Engineering,” NASA TT F-223, 1965.
  9. R. Zubrin, “Dipole Drive for Space Propulsion,” JBIS, 70, 2017, pp. 442- 448.
  10. D. Brisbin, “Spacecraft with Interstellar Medium Momentum Exchange Reactions: The Potential and Limitations of Propellantless Interstellar Travel,” JBIS, Vol 72, pp 116-124, 2019
  11. K. Tsiolkovsky, “The Exploration of Cosmic Space by Means of Reaction Devices”, The Science Review (Nauchnoye Obozreniye), May 1903, from translation “Collected Works of K.E. Tsiolkovsky: Volume II – Reactive Flying Machines” NASA TT F-237, 1965, pp 72-117.
  12. R. W. Bussard, “Galactic Matter and Interstellar Flight”, Acta Astronautica, 6, 1960, pp. 179-194.
  13. T.A. Heppenheimer, “On the Infeasibility of Interstellar Ramjets”, JBIS, 31, 1978, p. 222ff
  14. R. Forward, “Alternate Propulsion Energy Sources,” Air Force Rocket Propulsion Laboratory, AFRPL TR-83-067, December 1983.
  15. M. Munk, “Notes on Propeller Design – IV”, NACA Technical Note No. 96, May, 1922, p. 6
  16. H. Oberth, Wege zur Raumschiffahrt, R. Oldenbourg Verlag, Munich- Berlin, 1929, in translation as “Ways to Spaceflight,” NASA TT F-622, 1970, pp. 217-229
  17. H. Hirsch, “Inertial Electrostatic Confinement of Ionized Fusion Gases”, Journal of Applied Physics, 38(11), 1967
  18. B. Wiegmann, J. Vaughn, T. Schneider, M. Bangham, and A. Heaton, “Findings from NASA’s 2015-2017 Electric Sail Propulsion System Investigations”, 31st Annual AIAA/USU Conference on Small Satellites, AIAA, Washington, DC 2018.
  19. S. Seifert and D. Altman, “A Comparison of Adiabatic and Isothermal Expansion Processes in Rocket Nozzles”, American Rocket Society Journal, May-June 1952, p. 159-162.
  20. C. B. Eom et. al., “High Critical Current Density and Enhanced Irreversibility Field in Superconducting MgB2 Thin Films”, Nature, 411, 31 May 2001, p. 558-560.
  21. A. Matsumodo et. al., “Evaluation of connectivity, flux pinning, and upper critical field contributions to the critical current density of bulk pure and SiC-alloyed MgB2,” Applied Physics Letters, 89(132508), 2006.
  22. M. Ranot and W.N. Kang, “MgB2 coated superconducting tapes with high critical current densities fabricated by hybrid physical-chemical vapor deposition,” Current Applied Physics, 12(2), 2012, pp 353-363.
  23. S. Humphries, Principles of Charged Particle Acceleration, Wiley, New York, 1986, p. 453

Received 5 April 2019

Approved 5 June 2019